目 录

1.1 随机试验与样本空间
随机试验E
定义 具有以下特点的试验称为随机试验
(1)可以在相同的条件下重复地进行
(2)每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;
(3)进行一次试验之前不能确定哪一个结果会出现。
样本空间
样本空间![]() 随机试验的所有可能结果组成的集合称为样本空间。
随机试验的所有可能结果组成的集合称为样本空间。
样本点![]() 样本空间的元素,即随机试验的每一可能结果称为样本点
样本空间的元素,即随机试验的每一可能结果称为样本点
样本空间的分类
① 有限集;② 无限可列集;③ 无限不可列集

1.2 随机事件
定义 样本空间![]() 的子集,通常用
的子集,通常用![]() ,
,![]() ,
,![]() 表示
表示
分类
① 基本事件 由一个样本点组成的单点集
② 复合事件 由至少两个基本事件组成
③ 必然事件 样本空间![]() 包含所有样本点,它是
包含所有样本点,它是![]() 自身的子集,在每次试验中它总是发生的,称为必然事件。记为
自身的子集,在每次试验中它总是发生的,称为必然事件。记为![]() 。
。
④ 不可能事件 空集![]() 不包含任何样本点,它也作为样本空间的子集,在每次试验中都不发生,称为不可能事件。记为
不包含任何样本点,它也作为样本空间的子集,在每次试验中都不发生,称为不可能事件。记为![]() 。
。
事件发生 在每次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件出现(发生)。
事件间的关系与运算
事件间的关系
(1)包含关系 ![]()
![]() 事件
事件![]() 发生一定导致
发生一定导致![]() 发生
发生
(2)事件相等 ![]() 且
且![]() ,则事件
,则事件![]()
(3) ![]() 和
和![]() 的和事件 记为
的和事件 记为![]()
![]() ,
,![]() 至少有一个
至少有一个

发生时事件![]() 发生。类似地,称
发生。类似地,称![]() 为
为![]() 个事件
个事件![]() 的和事件。
的和事件。
(4) ![]() 和
和![]() 的积事件 记为
的积事件 记为![]()
![]() ,
,![]() 同时发生时事件
同时发生时事件![]() 发生,类似地,称
发生,类似地,称![]() 为
为![]() 个事件
个事件![]() 的积事件。
的积事件。
(5)![]() 和
和![]() 的差事件 事件
的差事件 事件![]()
![]() 发生、
发生、![]() 不发生时事件
不发生时事件![]() 发生。也记为
发生。也记为![]() 。
。
(6)互斥(互不相容)事件 ![]()
![]()
![]() ,
,![]() 不能同时发生。
不能同时发生。
(7)对立(互逆)事件 ![]() 且
且![]()
![]()
![]() ,
,![]() 在一次试验中必然发生且只能发生一个。
在一次试验中必然发生且只能发生一个。![]() 的对立事件记为
的对立事件记为![]() 。
。
(8)完备事件组
若事件![]() ,则称事件
,则称事件![]() 是一个完备事件组。
是一个完备事件组。
事件的运算律
(1)交换律

![]()
(2)结合律 ![]() ;
;![]()
(3)分配律 ![]()
(4)德摩根律(对偶律) ![]()
随机事件的概率
古典概型及其概率计算
(1) 定义 具有以下两特点的试验称为古典概型
① 样本空间有限 ![]()
② 等可能性 ![]()
(2)计算方法 ![]()
(3)古典概率的性质
1)非负性 ![]() ,
,![]()
2)规范性![]()
3)有限可加性 设![]() 是两两互不相容的事件,即对于
是两两互不相容的事件,即对于

![]() 则有
则有![]()
几何概型的定义与计算
设随机试验的可能结果可以等可能地几何表示为某区域![]() 中的一点,且点落在区域
中的一点,且点落在区域![]() 的概率与
的概率与![]() 的测度(长度,面积,体积)成正比,而与
的测度(长度,面积,体积)成正比,而与![]() 的位置与形状无关,则该试验为几何概型。且
的位置与形状无关,则该试验为几何概型。且![]()
几何概率的性质
1)非负性 ![]() ,
,![]()
2)规范性 ![]()
3)可列可加性 设![]() 是两两互不相容的事件,即对于
是两两互不相容的事件,即对于![]() 则有
则有![]()
概率的公理化定义
定义 设![]() 是随机试验,
是随机试验,![]() 是它的样本空间,对于
是它的样本空间,对于![]() 的每一个
的每一个

事件![]() 赋予一个实数,记为
赋予一个实数,记为![]() ,称为事件
,称为事件![]() 的概率,如果集合函数
的概率,如果集合函数![]() 满足下列条件
满足下列条件
1)非负性 对于每一个事件![]() ,有
,有![]() ;
;
2)规范性 对于必然事件![]() ,有
,有![]()
3)可列可加性 设![]() 是两两互不相容的事件,即对于
是两两互不相容的事件,即对于![]() 则有
则有![]()
概率的性质
1)非负性 ![]() ,
,![]()
2)规范性 ![]()
3)有限可加性 设![]() 是两两互不相容的事件,即对于
是两两互不相容的事件,即对于![]() 则有
则有
![]()
4)逆事件的概率 对于任一事件![]() ,有
,有![]()
5)可比性 设![]() 是两个事件,若
是两个事件,若![]() ,则有
,则有

![]()
![]()
6)加法公式 对于任意两随机事件![]() 有
有![]()
定义 设![]() 是两个事件,且
是两个事件,且![]() ,称
,称 ![]() 为在事件
为在事件![]() 发生的条件下事件
发生的条件下事件![]() 发生的条件概率。
发生的条件概率。
条件概率的性质(与概率的性质相同)
1)![]() ;
;
2)![]() ;
;
3)![]()
4)![]()
5)乘法公式 ![]()
推广 设![]() 为事件,且
为事件,且![]() ,则有
,则有![]()

事件的独立性
定义 设![]() 是两个事件,如果满足等式
是两个事件,如果满足等式 ![]() ,则称事件
,则称事件![]() 相互独立,简称事件
相互独立,简称事件![]() 独立。
独立。
独立的等价说法
若![]() ,则事件
,则事件![]() 独立
独立
![]()
![]()
![]()
![]()
独立的性质
若事件![]() 相互独立,则
相互独立,则![]() ,
,![]() ,
,![]() 也相互独立。
也相互独立。
三个事件的独立性 设![]() 是三个事件,如果满足等式
是三个事件,如果满足等式
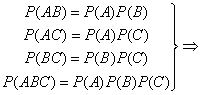
![]() 相互独立。
相互独立。
全概率公式

![]() 是完备事件组,且
是完备事件组,且![]() 则
则
![]()
贝叶斯公式(逆概公式)
![]() 是完备事件组,
是完备事件组,![]()
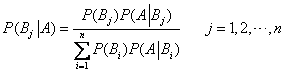
![]() 重伯努利概型及其概率计算
重伯努利概型及其概率计算
定义 只有两个结果![]() 的试验称为伯努利试验,若将伯努利试验独立重复地进行
的试验称为伯努利试验,若将伯努利试验独立重复地进行![]() 次,则称为
次,则称为![]() 重伯努利概型。
重伯努利概型。
计算公式
设在每次实验中,事件![]() 发生的概率
发生的概率![]() ,事件
,事件![]() 不发生的概率为
不发生的概率为![]() (
(![]() ),则在
),则在![]() 重伯努利实验中,事件
重伯努利实验中,事件![]() 发生
发生![]() 次的概率记为
次的概率记为![]() 。
。

1.3 重要公式与结论
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(5)条件概率![]() 满足概率的所有性质,
满足概率的所有性质,
例如 ![]()
![]()
![]()
(6)若![]() 相互独立,则
相互独立,则![]()
(7)互斥、互逆与独立性之间的关系 A与B互逆![]() A与B互斥,但反之不成立,A与B互斥(或互逆)且均非零概率事件
A与B互斥,但反之不成立,A与B互斥(或互逆)且均非零概率事件![]() A
A

2.1 随机变量
随机变量的定义 在样本空间![]() 上的实值函数
上的实值函数![]()
![]() ,则该变量
,则该变量![]() 称为随机变量. 随机变量常用大写字母
称为随机变量. 随机变量常用大写字母![]() 等表示,即
等表示,即![]() ,其取值用小写字母
,其取值用小写字母![]() 等表示。
等表示。
随机变量的分类
(1)离散型随机变量![]() 的取值为有限个或无限可列个
的取值为有限个或无限可列个
(2)连续型随机变量![]() 的取值为某区间上的所有值
的取值为某区间上的所有值
(3)非离散型也非连续型
2.2 离散型随机变量
定义 设![]() 为离散型随机变量,其可能取值为
为离散型随机变量,其可能取值为![]() ,
,![]() 取各个值
取各个值![]() 的概率为
的概率为![]() ,其中
,其中
1) ![]()
![]()
2)

![]()
则称![]() 为随机变量
为随机变量![]() 的概率分布或分布律,也可记为
的概率分布或分布律,也可记为

常用离散型随机变量
(1)二项分布 ![]()
设事件![]() 在任意一次实验中出现的概率都是
在任意一次实验中出现的概率都是![]() (
(![]() )
)![]() 表示
表示![]() 重贝努利试验中事件A发生的次数,则
重贝努利试验中事件A发生的次数,则![]() 所有可能的取值为
所有可能的取值为![]() ,且相应的概率为
,且相应的概率为![]()
![]() ,
,![]()
(2)![]() 分布 (二项分布的特例)
分布 (二项分布的特例)
若随机变量![]() 只有两个可能的取值0和1,其概率分布为
只有两个可能的取值0和1,其概率分布为

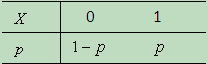
或 ![]() 则称
则称![]() 服从
服从![]() 分布。
分布。
(3)泊松分布 (二项分布的极限分布)
设随机变量![]() 的概率分布为
的概率分布为 ![]() 则称
则称![]() 服从参数为
服从参数为![]() 的泊松分布,记为
的泊松分布,记为![]()
注 ![]() 其中
其中![]()
随机变量的分布函数
定义 设![]() 是一个随机变量,对于任意实数
是一个随机变量,对于任意实数![]() ,令
,令![]() 称
称![]() 为随机变量X的概率分布函数,简称分布函数
为随机变量X的概率分布函数,简称分布函数

.
分布函数的性质
(1)非负性 ![]()
(2)规范性 ![]()
(3)单调不减性 对于任意![]() ,有
,有![]() ;
;
(4)右连续性 ![]()
利用分布函数求各种随机事件的概率
已知 ![]() 则有
则有
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()
(6)![]()
(7)

![]()
(8)![]()
离散型随机变量的分布函数
定义 ![]()
![]()
2.3 连续型随机变量的概率分布
概率密度函数
如果对于随机变量![]() 的分布函数
的分布函数![]() ,存在非负可积函数
,存在非负可积函数![]()
![]() ,使得对于任意实数
,使得对于任意实数![]() ,有
,有![]() 则称
则称![]() 为连续型随机变量,函数
为连续型随机变量,函数![]() 称为
称为![]() 的概率密度函数(简称密度函数)。
的概率密度函数(简称密度函数)。
性质
(1)非负性 ![]() (
(![]() );
);

(2)规范性 ![]() =
=![]() 1;
1;
(3)对于任意实数![]() 和
和![]() ,有
,有![]() ;
;
(4)在![]() 的连续点处,有
的连续点处,有![]()
(5)连续型随机变量的分布函数![]() 是连续函数。
是连续函数。
(6)对于连续型随机变量![]() ,
,![]() ,对
,对![]() 成立。
成立。
常用连续型随机变量
1)均匀分布 ![]() (几何概型)
(几何概型)
如果随机变量![]() ,其密度函数为
,其密度函数为 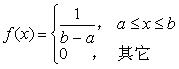 则称
则称![]() 服从
服从![]() 上的均匀分布,记作
上的均匀分布,记作![]() .其中
.其中![]() 是
是

分布的参数。
![]() 的分布函数为
的分布函数为 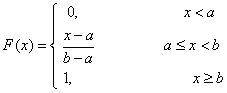
(2)指数分布 ![]() (寿命问题)
(寿命问题)
如果随机变量![]() ,其密度函数为
,其密度函数为 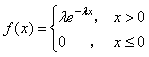
其中![]() 为参数,则称
为参数,则称![]() 服从参数为
服从参数为![]() 的指数分布,记作
的指数分布,记作![]() 。
。
指数分布的分布函数 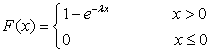
(3)正态分布
1)一般正态分布
一个连续型随机变量![]() ,如果其密度函数为
,如果其密度函数为

![]()
其中![]() 为常数,
为常数,![]() ,
,![]() ,则称
,则称![]() 服从参数为
服从参数为![]() 和
和![]() 的正态分布,记作
的正态分布,记作![]() .
.
2)标准正态分布
定义 当![]() ,
,![]() 的正态分布称为标准正态分布,记作
的正态分布称为标准正态分布,记作![]() ,其密度函数用
,其密度函数用![]() 表示,分布函数用
表示,分布函数用![]() 表示。其中
表示。其中![]()
性质
① ![]() 关于
关于![]() 轴对称;
轴对称;
② ![]()
③ ![]() ;
;
④ ![]()
查标准正态分布表
设![]() ,对于给定的
,对于给定的![]() ,如果
,如果![]() 满足条件
满足条件

![]() ,则称
,则称![]() 为标准正态分布的
为标准正态分布的![]() 分位点。由于
分位点。由于![]() ,因此可以利用标准正态分布表查出
,因此可以利用标准正态分布表查出![]() 的值。
的值。
3)标准正态分布与一般正态分布的关系(标准化)
一般正态分布![]() ,可以通过线性变换
,可以通过线性变换![]() 转化为标准正态分布。
转化为标准正态分布。
随机变量函数的分布
1、离散型随机变量的函数分布
设![]() 是离散型随机变量,概率分布为
是离散型随机变量,概率分布为![]() 则随机变量
则随机变量![]() 的函数
的函数![]() 取值
取值![]() 的概率为
的概率为![]() 如果
如果![]() 中出现相同的函数值,则将它们相应的概率之和作为随机变量
中出现相同的函数值,则将它们相应的概率之和作为随机变量![]() 取该值的概率,就可以得到
取该值的概率,就可以得到![]() 的概率分布。
的概率分布。
2、连续型随机变量函数的概率密度
已知![]() ,求
,求![]()

方法 分布函数法
先求![]() 再求
再求![]()
两种情形
(1)![]() 为单调函数;
为单调函数;
(2)![]() 为非单调函数
为非单调函数
2.4 重要公式与结论
![]()
![]()
![]()
![]()
![]()
(5)离散型随机变量的分布函数为阶梯间断函数;连续型随机变量的分布函数为连续函数,但不一定为处处可导函数。
(6)存在既非离散也非连续型随机变量。

3.1 二维随机变量及其分布函数
二维随机变量 设![]() 是定义在样本空间
是定义在样本空间![]() 上的两个随机变量,则称向量
上的两个随机变量,则称向量![]() 为二维随机变量(或随机向量)
为二维随机变量(或随机向量)
二维随机变量分布函数的定义 设![]() 是二维随机变量,对于任意实数
是二维随机变量,对于任意实数![]() ,称二元函数
,称二元函数 ![]()
![]() 为二维随机变量
为二维随机变量![]() 的分布函数或随机变量
的分布函数或随机变量![]() 与
与![]() 的联合分布函数,它表示随机事件
的联合分布函数,它表示随机事件![]() 与
与![]() 同时发生的概率.
同时发生的概率.
二维随机变量分布函数的性质
(1)非负性 对于任意实数![]() ,
,![]() ;
;
(2)规范性 ![]() ;
;![]()

![]()
(3)不减性 ![]() 分别关于
分别关于![]() 和
和![]() 单调不减;
单调不减;
(4)右连续性 ![]() 分别关于
分别关于![]() 和
和![]() 右连续,即
右连续,即
![]()
![]()
二维随机变量的边缘分布函数
设二维随机变量![]() 的分布函数为
的分布函数为![]() ,分别称
,分别称
![]()
同理 ![]() 为
为![]() 关于
关于![]() 和关于
和关于![]() 的边缘分布函数。
的边缘分布函数。
二维随机变量的独立性
设二维随机变量![]() 的分布函数为
的分布函数为![]() ,关于
,关于![]() 和关于
和关于![]() 的分布函数分别为
的分布函数分别为![]() 和
和![]() ,如果对于任意实数
,如果对于任意实数![]() 和
和![]() 有:
有:![]() ,则称随机变量
,则称随机变量![]() 和
和![]() 相互独立。
相互独立。

3.2 二维离散型随机变量
二维离散型随机变量定义 如果二维随机变量![]() 可能取的值为有限对或无限可列多对实数,则称
可能取的值为有限对或无限可列多对实数,则称![]() 为二维离散型随机变量.
为二维离散型随机变量.
联合分布律 设二维离散型随机变量![]() 所有可能的取值为
所有可能的取值为![]() ,且对应的概率为
,且对应的概率为 ![]() 其中:
其中:![]() ,且
,且![]() ,则称为二维离散型随机变量
,则称为二维离散型随机变量![]() 的概率分布或随机变量
的概率分布或随机变量![]() 和
和![]() 的联合概率分布。
的联合概率分布。
边缘分布律 对于二维离散型随机变量![]() ,设其概率分布为
,设其概率分布为![]()
则![]() 的边缘分布为:
的边缘分布为:

![]()
![]() 的边缘分布为:
的边缘分布为:
![]()
边缘分布函数:
![]()
![]()
条件分布律
设二维离散型随机变量![]() 的概率分布为
的概率分布为
![]()
![]()
(1)对于给定的![]() ,如果
,如果![]() ,则称
,则称

 为在
为在![]() 条件下随机变量
条件下随机变量![]() 的条件概率分布。
的条件概率分布。
(2)对于给定的![]() ,如果
,如果![]() ,则称
,则称
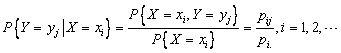 为在
为在![]() 条件下随机变量
条件下随机变量![]() 的条件概率分布。
的条件概率分布。
离散型随机变量![]() 与
与![]() 的独立性
的独立性
如果![]() 是二维离散型随机变量,则随机变量
是二维离散型随机变量,则随机变量![]() 和
和![]() 相互独立的充分必要条件是
相互独立的充分必要条件是![]() 即
即 ![]() ,
,![]()
3.3 二维连续型随机变量
定义 设二维随机变量![]() 的分布函数为
的分布函数为![]() ,如果存在非
,如果存在非

负可积的二元函数![]() ,使得对任意实数
,使得对任意实数![]() ,有
,有![]() ,则称
,则称![]() 为二维连续型随机变量,称函数
为二维连续型随机变量,称函数![]() 为二维随机变量
为二维随机变量![]() 的概率密度函数或随机变量
的概率密度函数或随机变量![]() 和
和![]() 的联合密度函数.
的联合密度函数.
性质
(1)![]() ;
;
(2)![]() ;
;
(3)若![]() 在点
在点![]() 处连续,则有
处连续,则有![]() ;
;
(4)设![]() 是
是![]() 平面上任一区域,则点
平面上任一区域,则点![]() 落在
落在![]() 内的概率为:
内的概率为:
![]()
边缘概率密度 设![]() 为连续型随机变量,它的概率密度函数
为连续型随机变量,它的概率密度函数

为![]() ,则
,则
![]() 的缘密度函数为:
的缘密度函数为:![]()
![]() 的边缘密度函数为:
的边缘密度函数为:![]()
二维连续型随机变量的条件概率密度
设二维随机变量![]() 的概率密度为
的概率密度为![]()
(1)对于给定的实数![]() ,边缘概率密度
,边缘概率密度![]() ,则称
,则称![]() 为在条件
为在条件![]() 下
下![]() 的条件概率密度函数
的条件概率密度函数
(2)对于给定的实数![]() ,边缘概率密度
,边缘概率密度![]() ,则称
,则称![]() 为在条件
为在条件![]() 下
下![]() 的条件概率密度函数
的条件概率密度函数
二维连续型随机变量的独立性 如果二维随机变量![]() 的联合密度为
的联合密度为![]() ,边缘概率密度分别为
,边缘概率密度分别为![]() 和
和![]() ,则随机变量
,则随机变量![]() 和
和![]() 相互独立的充要条件是,对一切
相互独立的充要条件是,对一切![]() 均有
均有![]()

两个常见的二维连续型随机变量的分布
(1)二维均匀分布 设![]() 是平面上有界可求面积的区域,其面积为
是平面上有界可求面积的区域,其面积为![]() ,若二维随机变量
,若二维随机变量![]() 具有密度函数
具有密度函数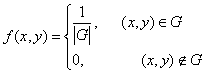 则称
则称![]() 服从区域
服从区域![]() 上的二维均匀分布.
上的二维均匀分布.
性质 若在各边平行于坐标轴的矩形区域![]() 上服从均匀分布的随机变量
上服从均匀分布的随机变量![]() ,则它的两个分量
,则它的两个分量![]() 和
和![]() 是独立的,并且分别服从区间
是独立的,并且分别服从区间![]() 上的一维均匀分布。
上的一维均匀分布。
(2)二维正态分布 如果二维连续型随机变量![]() 的概率密度为:
的概率密度为:

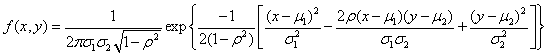
![]() ,其中
,其中![]() 均为常数,则称
均为常数,则称![]() 服从参数为
服从参数为![]() 和
和![]() 的二维正态分布,记作
的二维正态分布,记作 ![]() ,也称
,也称![]() 为二维正态随机变量。
为二维正态随机变量。
3.4 二维随机变量函数的分布
离散情形 已知![]() 的联合分布律为
的联合分布律为
![]()

注意:![]() 的分布律中,如果表中函数值有重复的只取一次,对应概率相加即可。
的分布律中,如果表中函数值有重复的只取一次,对应概率相加即可。
连续情形

分布函数法
设二维连续型随机变量![]() 的概率密度为
的概率密度为![]() ,则随机变量的函数
,则随机变量的函数![]() 的分布函数为:
的分布函数为:
![]()
(1)![]() ,则
,则![]() 的分布函数为:
的分布函数为:
![]() ,
,
由此可得![]() 的概率密度为:
的概率密度为:![]() 或
或![]() 如果随机变量
如果随机变量![]() 独立,
独立,![]() 关于
关于![]() 的边缘概率密度分别为
的边缘概率密度分别为![]() ,
,![]() 则上式可化为:
则上式可化为:![]() 或
或 ![]() 这个公式称为独立和卷积公式。
这个公式称为独立和卷积公式。

![]()
![]() ;
;![]()
协方差 ![]()
相关系数
![]() ,
,
![]() 阶原点矩
阶原点矩 ![]() ;
;
![]() 阶中心矩
阶中心矩 ![]()
性质
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()

切比雪夫不等式 ![]() 或
或![]()
切比雪夫大数定律 设![]() 相互独立,且
相互独立,且
![]() 则对于任意正数
则对于任意正数![]() ,有
,有
![]()
依概率收敛 设![]() 是一个随机变量序列,
是一个随机变量序列,![]() 是一个常数,如果对于任意给定的正数
是一个常数,如果对于任意给定的正数![]() ,有
,有![]() 则称随机变量序列
则称随机变量序列![]() 依概率收敛于
依概率收敛于![]() ,记作
,记作![]()
伯努利大数定律 设![]() 相互独立,同
相互独立,同![]() 分布
分布![]() ,则对任意正数
,则对任意正数![]() ,有
,有![]()

6.1 总体和样本
总体 研究对象的某项数量指标的全体,它是一个随机变量,用![]() 表示
表示
个体 组成总体的每个基本元素
简单随机样本 来自总体![]() 的n个相互独立且与总体同分布的随机变量
的n个相互独立且与总体同分布的随机变量![]() 称为容量为n的简单随机样本,简称样本
称为容量为n的简单随机样本,简称样本
统计量 设![]() 是来自总体
是来自总体![]() 的一个样本,
的一个样本,![]() )是样本的连续函数,且
)是样本的连续函数,且![]() 中不含任何未知参数,则称
中不含任何未知参数,则称![]() 为统计量
为统计量
样本均值 ![]()
样本方差 ![]()

样本矩 样本k阶原点矩 ![]()
样本k阶中心矩 ![]()
顺序统计量 ![]() 和
和![]() 的分布
的分布
设总体![]() 分布函数为
分布函数为![]() ,
,![]() 是来自总体
是来自总体![]() 的样本,则统计量
的样本,则统计量![]() 和
和![]() 的分布函数分别为
的分布函数分别为
![]()
![]()
6.2 常用统计量的抽样分布
![]() 分布
分布
(1)典型模式
设随机变量![]() 相互独立,都服从标准正态分布
相互独立,都服从标准正态分布

![]() ,则随机变量
,则随机变量![]() 的概率密度为
的概率密度为
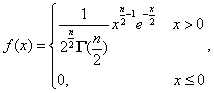
则称随机变量![]() 服从自由度为
服从自由度为![]() 的
的![]() 分布,记作
分布,记作![]() 。
。
(2)![]() 分布的性质
分布的性质
设![]() ,并且
,并且![]() 和
和![]() 相互独立,则
相互独立,则![]()
(3)上![]() 分位点
分位点![]()
设![]() ,对于任给定的
,对于任给定的![]() ,称满足条件
,称满足条件![]() 的点
的点![]() 为
为![]() 的上
的上![]() 分位点。
分位点。
![]() 分布
分布
(1)典型模式

设随机变量![]() ,且相互独立,则随机变量
,且相互独立,则随机变量![]() 服从自由度为
服从自由度为![]() 的
的![]() 分布(学生氏t分布),记作
分布(学生氏t分布),记作![]() .其分布密度函数为
.其分布密度函数为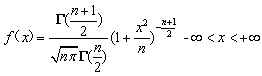
(2)![]() 分布的性质
分布的性质
![]() 分布的概率密度
分布的概率密度![]() 是偶函数且有
是偶函数且有![]() 即当
即当![]() 充分大时,
充分大时,![]() 分布近似
分布近似![]() 分布。
分布。
(3)上![]() 分位点
分位点![]()
设![]() ,对于任给定的
,对于任给定的![]() ,称满足条件
,称满足条件![]() 的点
的点![]() 为
为![]() 的上
的上![]() 分位点。由于
分位点。由于![]() 分布的概率密度是偶函数,因此
分布的概率密度是偶函数,因此![]()

![]() 分布
分布
(1)典型模式
设随机变量![]() 相互独立,且
相互独立,且![]()
![]() ,则随机变量
,则随机变量![]() 服从自由度为
服从自由度为![]() 的
的![]() 分布,记作
分布,记作![]() ,其分布密度函数为
,其分布密度函数为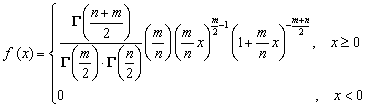
(2)![]() 分布的性质 设
分布的性质 设![]() ,则
,则![]() ;
;
(3)上![]() 分位点
分位点![]()
设![]() ,对于任给定的
,对于任给定的![]() ,称满足条件
,称满足条件![]() 的点
的点![]() 为
为![]() 的上
的上![]() 分位点,且有
分位点,且有

设![]() ,
,![]() 和
和![]() ,分别来自总体
,分别来自总体![]() 的样本,且两个总体相互独立,则有
的样本,且两个总体相互独立,则有
(1)![]() ,
,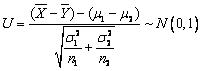
(2)如果![]() 则
则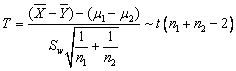 其中
其中
![]()
(3)

7.1 点估计的概念,估计量与估计值,矩估计法,最大似然估计法
(1)![]() 为
为![]() 的矩估计, g(x)为连续函数,则g(
的矩估计, g(x)为连续函数,则g(![]() )为g(
)为g(![]() )的矩估计。
)的矩估计。
(2)![]() 为
为![]() 的极大似数估计,g(x)为单调函数,则
的极大似数估计,g(x)为单调函数,则![]() 为
为![]() 的极大似然估计
的极大似然估计
(3)![]() 即
即![]() ,
,![]() 分别为总体
分别为总体![]()
![]() 的无偏估计量。
的无偏估计量。
(4)由大数定律易知![]() ,
,![]() 也分别是
也分别是![]()
![]() 的一致估量。
的一致估量。
(5)若![]() 则
则![]() 为
为![]() 的一致估计。
的一致估计。
7.2 估计量的评选标准区间估计的概念
(1)估计量的选取标准:无偏性、有效性、相合性
(2)![]() 为
为![]() 的置信度是
的置信度是![]() 的置信区间,g(x)为单调增加(或单调减少)函数,则
的置信区间,g(x)为单调增加(或单调减少)函数,则![]() 为
为![]() 的
的

置信度是![]() 的置信区间
的置信区间
(3)单个正态总体的均值和方差的区间估计,两个正态总体的均值差和方差比的区间估计
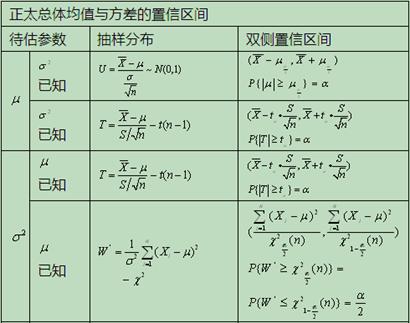

8.1 显著性检验,假设检验的两类错误
假设检验的一般步骤
(1)确定所要检验的基本假设![]() ;
;
(2)选择检验的统计量,并要求知道其在一定条件下的分布;
(3)对确定的显著性水平![]() ,查相应的概率分布,得临界值,从而确定否定域;
,查相应的概率分布,得临界值,从而确定否定域;
(4)由样本计算统计量,并判断其是否落入否定域,从而对假设![]() 作出拒绝还是接受的判断
作出拒绝还是接受的判断
假设检验的两类错误
统计推断是由样本推断总体,所作的结论不能保证绝对不犯错误,而只能以较大概率来保证其可靠性。
第一类错误是否定了真实的假设,即假设本来成立,但被错误地否认了,成为“弃真”,检验水平![]() 就是犯第一类错误的概率的最大允许值。
就是犯第一类错误的概率的最大允许值。
第二类错误是把本来不成立的假设错误地接受了,称为“存伪”。犯这类错误的大小一般用![]() 表示,它的大小要视具体情况
表示,它的大小要视具体情况

设 ![]() ----首项,
----首项,![]() ----通项,
----通项,![]() ----公差,
----公差,![]() ----前n项和
----前n项和
![]() ;
;
![]() ;
;
![]()
(2)等比数列
设![]() ----首项,q----公比,
----首项,q----公比,![]() ----通项,则
----通项,则
![]() ;
;
![]()
(3)常用的几种数列的和
![]()

![]()
![]()
![]()
![]()
6)![]()
7) ![]()
8) ![]()
2. 两个基本原理
(1)乘法原理:完成某事要![]() 个步骤,每一步有
个步骤,每一步有![]() 种方法,则完成此事共有
种方法,则完成此事共有![]() 种方法。
种方法。

(2)加法原理:完成某事有![]() 类方法,每一类分别有
类方法,每一类分别有![]() 种,则完成此事共有
种,则完成此事共有![]() 种方法。
种方法。
3. 排列
(1)定义:从![]() 个不同的元素种任取
个不同的元素种任取![]() 个(
个(![]() ),按一定顺序排成一列,则称为从
),按一定顺序排成一列,则称为从![]() 个元素中取出
个元素中取出![]() 个元素的一个排列,其个数记为
个元素的一个排列,其个数记为![]() 或
或![]()
(2)排列的种类及计算公式
① 选排列 ![]() (
(![]() )
)
② 全排列 (![]() )
) ![]()
③ 有重复的排列 ![]()
4. 组合
(1)定义 从![]() 个不同的元素种任取
个不同的元素种任取![]() 个(
个(![]() ),不计顺序拼成一组,称为从
),不计顺序拼成一组,称为从![]() 个元素中取出
个元素中取出![]() 个元素的组合,记为
个元素的组合,记为![]()
(2)计算公式 ![]()
(3)性质:![]() ,
,![]()

注:排列有序,组合无序
(4)二项式定理
![]()
跳转至 GO页,共60页
